【DFSBFS】2024D-图像物体的边界
【DFSBFS】2024D-图像物体的边界
题目描述与示例
本题练习地址:https://www.algomooc.com/problem/P3499
题目描述
给定一个二维数组M行N列,二维数组里的数字代表图片的像素,为了简化问题,仅包含像素1和5两种像素,每种像素代表一个物体,2个物体相邻的格子为边界,求像素1代表的物体的边界个数。
像素1代表的物体的边界指与像素5相邻的像素1的格子,边界相邻的属于同一个边界,相邻需要考虑8个方向(上,下,左,右,左上,左下,右上,右下)
其他约束:
地图规格约束为:
0<M<100
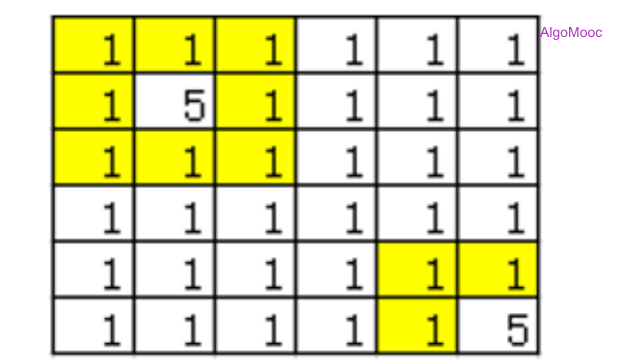
0<N<1001、如下图,与像素5的格子相邻的像素1的格子(0,0)、(0,1)、(0,2)、(1,0)、(1,2)、(2,0)、(2,1)、(2,2)、(4,4)、(4,5)、(5,4)为边界,另(0,0)、(0,1)、(0,2)、(1,0)、(1,2)、(2,0)、(2,1)、(2,2)相邻,为1个边界,(4,4)、(4,5)、(5,4)相邻,为1个边界,所以下图边界个数为2。
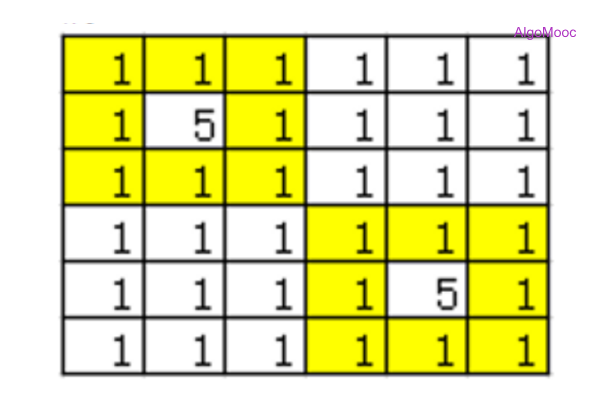
2、如下图,与像素5的格子相邻的像素1的格子(0,0)、(0,1)、(0,2)、(1,0)、(1,2)、(2,0)、(2,1)、(2,2)、(3,3)、(3,4)、(3,5)、(4,3)、(4,5)、(5,3)、(5,4)、(5,5)为边界,另这些边界相邻,所以下图边界个数为1。注:(2,2)、(3,3)相邻
输入描述
第一行,行数M,列数N
第二行开始,是M行N列的像素的二维数组,仅包含像素1和5
输出描述
像素1代表的物体的边界个数。如果没有边界输出0(比如只存在像素1,或者只存在像素5)
示例
输入
6 6
1 1 1 1 1 1
1 5 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 5输出
2解题思路
预处理原始数据
首先需要需要对原始数据进行预处理。
将所有5周围的像素点都标记出来,可以使用除了1和5之外的其他数字来标记,比如3。譬如,把
1 1 1 1 1 1
1 5 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 5标注成
3 3 3 1 1 1
3 5 3 1 1 1
3 3 3 1 1 1
1 1 1 1 1 1
1 1 1 1 3 3
1 1 1 1 3 5其相关代码如下
DIRECTIONS = [(0,1), (1,0), (-1,0), (0,-1), (1,1), (1,-1), (-1,1), (-1,-1)]
for i in range(n):
for j in range(m):
if grid[i][j] == 5:
for di, dj in DIRECTIONS:
ni, nj = i+di, j+dy
if 0 <= ni < n and 0 <= nj < m and grid[ni][nj] == 1:
grid[ni][nj] = 3剩余内容就是常规地套模板,进行DFS或者BFS。
本题需要计算边界个数,即为计算连通块个数,和LeetCode200、岛屿数量 的要求类似。
代码
解法一:DFS
Python
# 题目:2023C-图像物体的边界
# 分值:200
# 作者:闭着眼睛学数理化
# 算法:DFS
# 代码看不懂的地方,请直接在群上提问
# dfs函数,套模板即可
def dfs(grid, check_list, i, j, n, m):
check_list[i][j] = 1
for di, dj in DIRECTIONS:
ni, nj = i+di, j+dj
if 0 <= ni < n and 0 <= nj < m and check_list[ni][nj] == 0 and grid[ni][nj] == 3:
dfs(grid, check_list, ni, nj, n, m)
# 八个方向所构成的数组
DIRECTIONS = [(0,1), (1,0), (-1,0), (0,-1), (1,1), (1,-1), (-1,1), (-1,-1)]
# 输入长、宽
n, m = map(int, input().split())
# 构建网格
grid = list()
for _ in range(n):
grid.append(list(map(int, input().split())))
# 预处理
# 遍历所有网格点,将5周围的边界都修改为3
for i in range(n):
for j in range(m):
if grid[i][j] == 5:
# 考虑5的周围的八个方向的近邻点(ni, nj)
for di, dj in DIRECTIONS:
ni, nj = i+di, j+dj
# 若(ni, nj)未越界,且值为1,则可以修改为3
if 0 <= ni < n and 0 <= nj < m and grid[ni][nj] == 1:
grid[ni][nj] = 3
ans = 0
check_list = [[0] * m for _ in range(n)]
# 从所有的3出发,进行深搜
for i in range(n):
for j in range(m):
if check_list[i][j] == 0 and grid[i][j] == 3:
# 每做完一次深搜,说明找到一个连通块,ans+1
dfs(grid, check_list, i, j, n, m)
ans += 1
print(ans)Java
import java.util.Scanner;
public class Main {
static int ans = 0;
static final int[][] DIRECTIONS = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
static void dfs(int[][] grid, int[][] checkList, int i, int j, int n, int m) {
checkList[i][j] = 1;
for (int[] dir : DIRECTIONS) {
int ni = i + dir[0];
int nj = j + dir[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < m && checkList[ni][nj] == 0 && grid[ni][nj] == 3) {
dfs(grid, checkList, ni, nj, n, m);
}
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
int[][] checkList = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
grid[i][j] = scanner.nextInt();
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 5) {
for (int[] dir : DIRECTIONS) {
int ni = i + dir[0];
int nj = j + dir[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < m && grid[ni][nj] == 1) {
grid[ni][nj] = 3;
}
}
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (checkList[i][j] == 0 && grid[i][j] == 3) {
dfs(grid, checkList, i, j, n, m);
ans++;
}
}
}
System.out.println(ans);
}
}C++
#include <iostream>
#include <vector>
using namespace std;
int ans = 0;
const vector<pair<int, int>> DIRECTIONS = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
void dfs(vector<vector<int>>& grid, vector<vector<int>>& checkList, int i, int j, int n, int m) {
checkList[i][j] = 1;
for (const auto& dir : DIRECTIONS) {
int ni = i + dir.first;
int nj = j + dir.second;
if (ni >= 0 && ni < n && nj >= 0 && nj < m && checkList[ni][nj] == 0 && grid[ni][nj] == 3) {
dfs(grid, checkList, ni, nj, n, m);
}
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m));
vector<vector<int>> checkList(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 5) {
for (const auto& dir : DIRECTIONS) {
int ni = i + dir.first;
int nj = j + dir.second;
if (ni >= 0 && ni < n && nj >= 0 && nj < m && grid[ni][nj] == 1) {
grid[ni][nj] = 3;
}
}
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (checkList[i][j] == 0 && grid[i][j] == 3) {
dfs(grid, checkList, i, j, n, m);
ans++;
}
}
}
cout << ans << endl;
return 0;
}解法二:BFS
Python
# 题目:2023C-图像物体的边界
# 分值:200
# 作者:闭着眼睛学数理化
# 算法:BFS
# 代码看不懂的地方,请直接在群上提问
from collections import deque
# 八个方向所构成的数组
DIRECTIONS = [(0,1), (1,0), (-1,0), (0,-1), (1,1), (1,-1), (-1,1), (-1,-1)]
# 输入长、宽
n, m = map(int, input().split())
# 构建网格
grid = list()
for _ in range(n):
grid.append(list(map(int, input().split())))
# 预处理
# 遍历所有网格点,将5周围的边界都修改为3
for i in range(n):
for j in range(m):
if grid[i][j] == 5:
# 考虑5的周围的八个方向的近邻点(ni, nj)
for di, dj in DIRECTIONS:
ni, nj = i+di, j+dj
# 若(ni, nj)未越界,且值为1,则可以修改为3
if 0 <= ni < n and 0 <= nj < m and grid[ni][nj] == 1:
grid[ni][nj] = 3
ans = 0
check_list = [[0] * m for _ in range(n)]
# 从所有的3出发,进行广搜
for i in range(n):
for j in range(m):
if check_list[i][j] == 0 and grid[i][j] == 3:
check_list[i][j] = 1
q = deque()
q.append((i, j))
while q:
ci, cj = q.popleft()
for di, dj in DIRECTIONS:
ni, nj = ci+di, cj+dj
if 0 <= ni < n and 0 <= nj < m and check_list[ni][nj] == 0 and grid[ni][nj] == 3:
check_list[ni][nj] = 1
q.append((ni, nj))
# 每做完一次广搜,说明找到一个连通块,ans+1
ans += 1
print(ans)Java
import java.util.*;
public class Main {
static final int[][] DIRECTIONS = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[][] grid = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
grid[i][j] = scanner.nextInt();
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 5) {
for (int[] dir : DIRECTIONS) {
int ni = i + dir[0];
int nj = j + dir[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < m && grid[ni][nj] == 1) {
grid[ni][nj] = 3;
}
}
}
}
}
int ans = 0;
int[][] checkList = new int[n][m];
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (checkList[i][j] == 0 && grid[i][j] == 3) {
checkList[i][j] = 1;
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{i, j});
while (!queue.isEmpty()) {
int[] cur = queue.poll();
for (int[] dir : DIRECTIONS) {
int ni = cur[0] + dir[0];
int nj = cur[1] + dir[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < m && checkList[ni][nj] == 0 && grid[ni][nj] == 3) {
checkList[ni][nj] = 1;
queue.offer(new int[]{ni, nj});
}
}
}
ans++;
}
}
}
System.out.println(ans);
}
}C++
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
vector<vector<int>> DIRECTIONS = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 5) {
for (auto& dir : DIRECTIONS) {
int ni = i + dir[0];
int nj = j + dir[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < m && grid[ni][nj] == 1) {
grid[ni][nj] = 3;
}
}
}
}
}
int ans = 0;
vector<vector<int>> checkList(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (checkList[i][j] == 0 && grid[i][j] == 3) {
checkList[i][j] = 1;
queue<pair<int, int>> q;
q.push({i, j});
while (!q.empty()) {
auto cur = q.front();
q.pop();
for (auto& dir : DIRECTIONS) {
int ni = cur.first + dir[0];
int nj = cur.second + dir[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < m && checkList[ni][nj] == 0 && grid[ni][nj] == 3) {
checkList[ni][nj] = 1;
q.push({ni, nj});
}
}
}
ans++;
}
}
}
cout << ans << endl;
return 0;
}时空复杂度
时间复杂度:O(NM)。
空间复杂度:O(NM)。
