2025A-生成哈夫曼树
题目描述与示例
题目描述
给定长度为n的无序的数字数组,每个数字代表二叉树的叶子节点的权值,数字数组的值均大于等于1。
请完成一个函数,根据输入的数字数组,生成哈夫曼树,并将哈夫曼树按照中序遍历输出。
为了保证输出的二又树中序遍历结果统一,增加以下限制:二叉树节点中,左节点权值小于等于右节点权值,根节点权值为左右节点权值之和。当左右节点权值相同时,左子树高度高度小于等于右子树
注意:所有用例保证有效,并能生成哈夫曼树。
提醒:哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。
例如:由叶子节点5 15 40 30 10生成的最优二叉树如下图所示
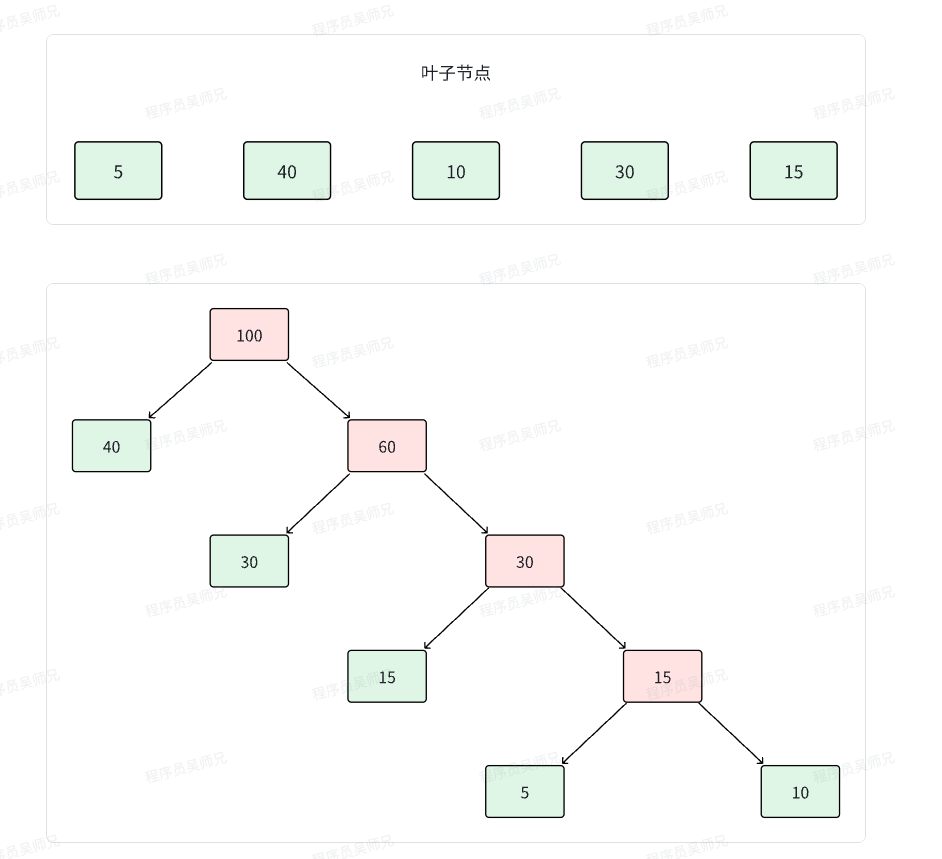
该树的最短带权路径长度为40*1+30*2+15*3+5*4+10*4 = 205
输入描述
第一行输入为数组长度,记为N,1<=N<=1000
第二行输入无序数值数组,以空格分割,数值均大于等于1,小于100000
输出描述
输出一个哈夫曼树的中序遍历的数组,数值间以空格分割
示例
输入
5
5 15 40 30 10输出
40 100 30 60 15 30 5 15 10解题思路
节点类的构建
普通的二叉树节点包括三个属性,值val,左节点left,右节点right。
但本题构建哈夫曼树的过程,还需要考虑到子树的高度,因此还需要储存一个高度height属性。
class TreeNode:
def __init__(self, val, left, right, height):
self.val = val
self.left = left
self.right = right
self.height = height构建哈夫曼树
本题的难点其实在于如何构建哈夫曼树。
具体例子
我们先看一个具体的例子。对于例子
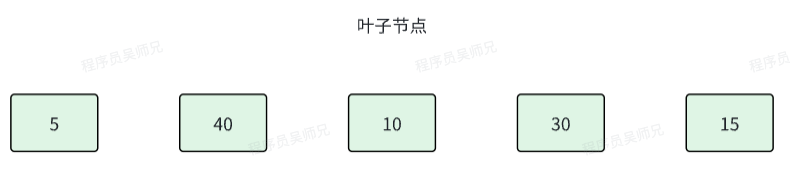
我们可以从叶节点开始进行哈夫曼树的构建,其过程如下。
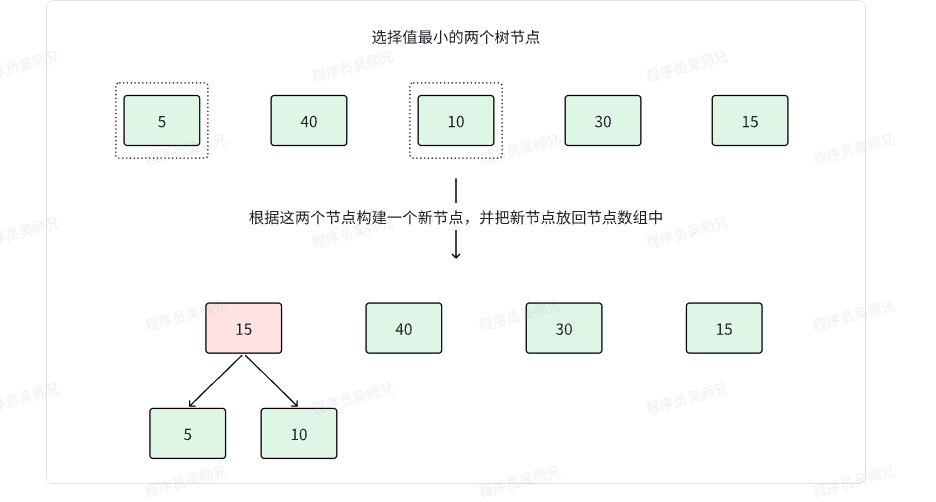
再重复上述过程
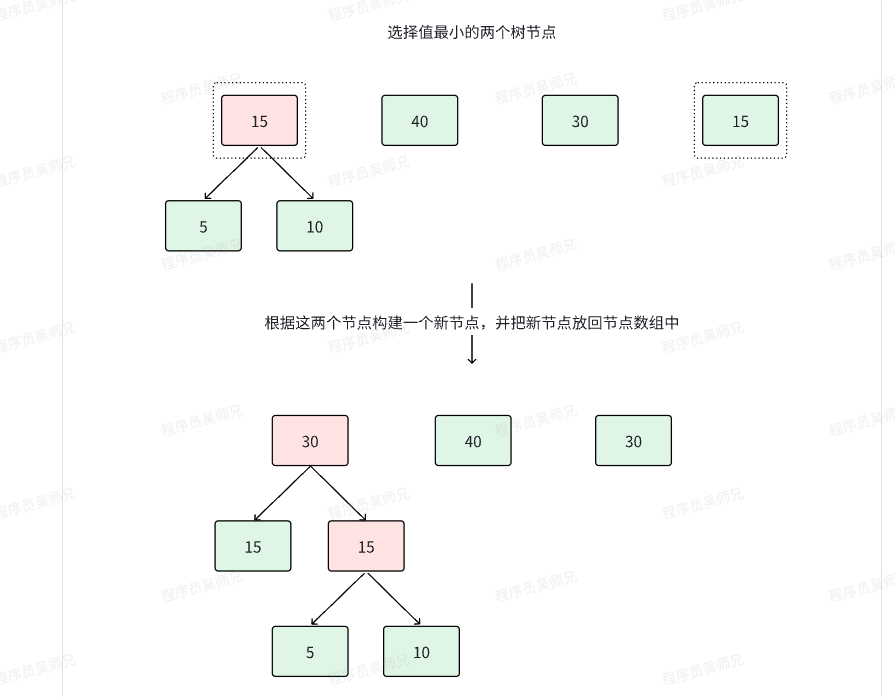
然后重复上述过程
构建树的逻辑
从上述例子可以窥见我们构建哈夫曼树的逻辑。
节点数组初始化
最开始的时候,我们需要构建一个节点数组,其中包含了所有的叶节点。
这些叶节点的左右节点均为None,高度为0。
node_lst = [TreeNode(val, None, None, 0) for val in lst]这些叶节点会是构建哈夫曼树的基础。
只考虑节点值来构建树
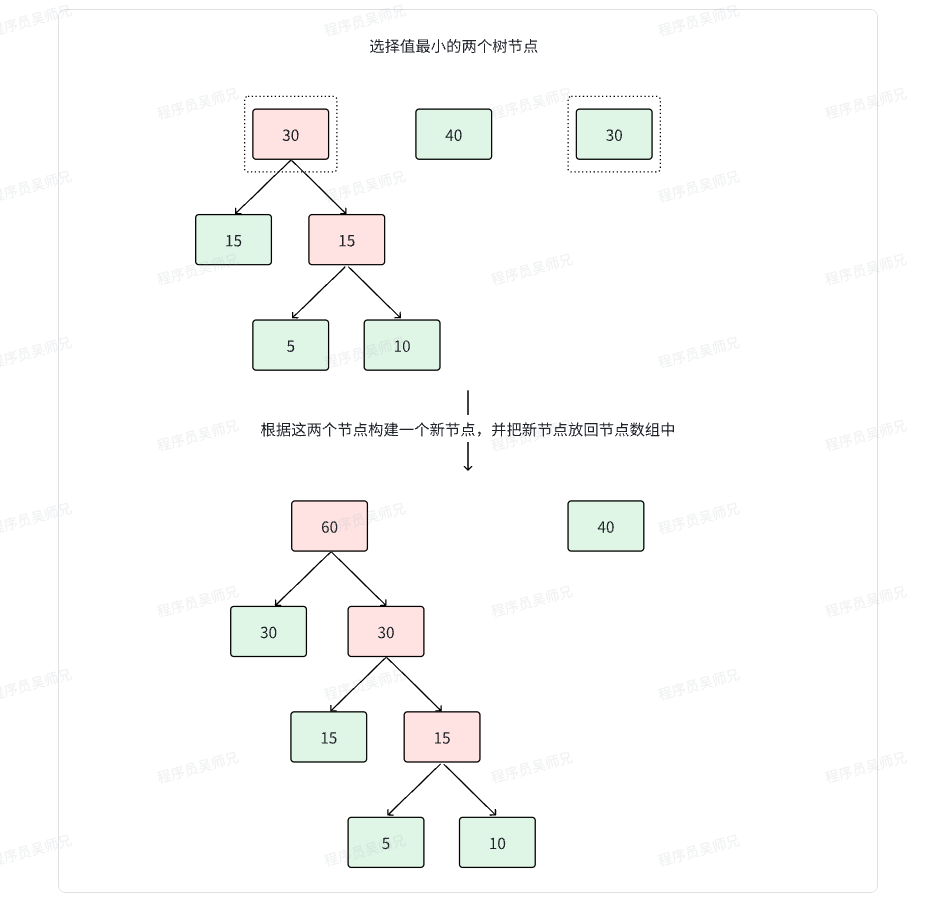
我们需要在node_lst中挑选出两个值最小的节点,根据这两个节点来构建一个新节点new_node。
由于需要挑选出值最小的两个节点,所以我们可以对node_lst进行排序。
node_lst.sort(key = lambda node: -node.val)
left, right = node_lst.pop(), node_lst.pop()新节点的值为这两个节点值的和,新节点的左节点为值较小的节点,新节点的右节点为值较大的节点。高度暂时先不考虑,设置为0。
val = left.val + right.val
new_node = TreeNode(val, left, right, 0)新节点需要重新加入node_lst,在后续这个节点会继续作为树中的节点来构建树
node_lst.append(new_node)同时考虑节点高度来构建树
在只考虑节点值的来构建树的过程中,我们默认了左节点的值是小于右节点的值的。
但题目中的描述存在这样一句话:当左右节点权值相同时,左子树高度高度小于等于右子树
这意味着左节点的值可能等于右节点的值,且在相等的时候我们需要同时考虑两棵子树的高度。
所以我们在对node_lst进行排序的时候,要同时考虑每一个节点的高度。
仍然优先按照节点值进行逆序排序,再按照高度进行逆序排序。修改代码
node_lst.sort(key=lambda node: (-node.val, -node.height))
left, right = node_lst.pop(), node_lst.pop()而新节点的高度height,等于弹出的两个左右节点的高度中的较大值再加1,其中加1表示新节点带来的新增高度。
height = max(left.height, right.height) + 1height也要作为属性来构建new_node。所以上述代码修改为
val = left.val + right.val
new_node = TreeNode(val, left, right, height)
node_lst.append(new_node)在循环中构建树
上述的流程只是构建了一棵子树,我们需要重复上述过程,直到构建出一棵完整的哈夫曼树。
那么构建到什么程度说明哈夫曼树完全构建完毕了呢?答案是当node_lst中只剩下一个节点的时候,那么这个剩下的唯一节点就是根节点。
因此整体的构建树的函数build_tree()如下
def build_tree(node_lst):
while (len(node_lst) > 1):
node_lst.sort(key=lambda node: (-node.val, -node.height))
left, right = node_lst.pop(), node_lst.pop()
val = left.val + right.val
height = max(left.height, right.height) + 1
new_node = TreeNode(val, left, right, height)
node_lst.append(new_node)中序遍历
构建完哈夫曼树之后,剩下的中序遍历就非常简单了。
在得到根节点root = node_lst[0]之后,直接套模板即可。
# 中序遍历递归函数
def inorder(ans, node):
if node == None:
return
inorder(ans, node.left)
ans.append(node.val)
inorder(ans, node.right)
# 构建哈夫曼树
node_lst = [TreeNode(val, None, None, 0) for val in lst]
build_tree(node_lst)
# 中序遍历,其中根节点为node_lst[0]
ans = list()
inorder(ans, node_lst[0])
# 输出答案
print(*ans)其他优化
上述解法已经是可以通过全部用例了,但如果想实现更优的时间复杂度,排序并取节点的这一步,可以用堆排序即优先队列来代替。
这样可以将构建树中while循环中的单步操作的时间复杂度从O(NlogN)降为O(logN)。
代码
Python
# 欢迎来到「欧弟算法 - 华为OD全攻略」,收录华为OD题库、面试指南、八股文与学员案例!
# 地址:https://www.odalgo.com
# 华为OD机试刷题网站:https://www.algomooc.com
# 添加微信 278166530 获取华为 OD 笔试真题题库和视频
# 定义树节点的类,包括
# 值val,左节点left,右节点right,该节点的高度(向下的层数)height
class TreeNode:
def __init__(self, val, left, right, height):
self.val = val
self.left = left
self.right = right
self.height = height
# 构建树的函数
def build_tree(node_lst):
# while循环,直到node_lst中只剩下一个节点,即为根节点
while (len(node_lst) > 1):
# 对node_lst进行排序,先按照节点值val逆序排序,再按照节点高度height逆序排序
node_lst.sort(key=lambda node: (-node.val, -node.height))
# 弹出末尾元素,为当前所选择的,用来构建新节点的两个节点
left, right = node_lst.pop(), node_lst.pop()
# 新节点的值为左右节点值的和
val = left.val + right.val
# 新节点的高度为左右节点的高度的较大值再+1
# 其中+1表示新节点增加的高度
height = max(left.height, right.height) + 1
# 构建新节点new_node
new_node = TreeNode(val, left, right, height)
# 将新节点加入列表new_node中
node_lst.append(new_node)
# 中序遍历的函数
def inorder(ans, node):
if node == None:
return
inorder(ans, node.left)
ans.append(node.val)
inorder(ans, node.right)
# 输入
n = int(input())
lst = list(map(int, input().split()))
# 初始化节点列表node_lst,包含为所有叶节点的列表
node_lst = [TreeNode(val, None, None, 0) for val in lst]
# 构建树,退出后node_lst的长度为1
build_tree(node_lst)
# 初始化答案列表
ans = list()
# 中序遍历函数,传入根节点为node_lst中唯一的一个节点node_lst[0]
inorder(ans, node_lst[0])
# 输出结果
print(*ans)Java
import java.util.*;
class TreeNode {
int val;
TreeNode left, right;
int height;
TreeNode(int val, TreeNode left, TreeNode right, int height) {
this.val = val;
this.left = left;
this.right = right;
this.height = height;
}
}
public class Main {
// 构建树的函数
public static void buildTree(List<TreeNode> nodeList) {
// while循环,直到node_lst中只剩下一个节点,即为根节点
while (nodeList.size() > 1) {
// 对node_lst进行排序,先按照节点值val逆序排序,再按照节点高度height逆序排序
nodeList.sort((a, b) -> {
if (b.val != a.val) return b.val - a.val;
return b.height - a.height;
});
// 弹出末尾元素,为当前所选择的,用来构建新节点的两个节点
TreeNode left = nodeList.remove(nodeList.size() - 1);
TreeNode right = nodeList.remove(nodeList.size() - 1);
// 新节点的值为左右节点值的和
int val = left.val + right.val;
// 新节点的高度为左右节点的高度的较大值再+1
// 其中+1表示新节点增加的高度
int height = Math.max(left.height, right.height) + 1;
// 构建新节点new_node
TreeNode newNode = new TreeNode(val, left, right, height);
// 将新节点加入列表new_node中
nodeList.add(newNode);
}
}
// 中序遍历的函数
public static void inorder(List<Integer> ans, TreeNode node) {
if (node == null) return;
inorder(ans, node.left);
ans.add(node.val);
inorder(ans, node.right);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] lst = new int[n];
for (int i = 0; i < n; i++) {
lst[i] = sc.nextInt();
}
// 初始化节点列表node_lst,包含为所有叶节点的列表
List<TreeNode> nodeList = new ArrayList<>();
for (int val : lst) {
nodeList.add(new TreeNode(val, null, null, 0));
}
// 构建树,退出后node_lst的长度为1
buildTree(nodeList);
// 初始化答案列表
List<Integer> ans = new ArrayList<>();
// 中序遍历函数,传入根节点为node_lst中唯一的一个节点node_lst.get(0)
inorder(ans, nodeList.get(0));
// 输出结果
for (int val : ans) {
System.out.print(val + " ");
}
}
}C++
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
class TreeNode {
public:
int val;
TreeNode* left;
TreeNode* right;
int height;
TreeNode(int val, TreeNode* left, TreeNode* right, int height) {
this->val = val;
this->left = left;
this->right = right;
this->height = height;
}
};
// 构建树的函数
void buildTree(vector<TreeNode*>& nodeList) {
// while循环,直到node_lst中只剩下一个节点,即为根节点
while (nodeList.size() > 1) {
// 对node_lst进行排序,先按照节点值val逆序排序,再按照节点高度height逆序排序
sort(nodeList.begin(), nodeList.end(), [](TreeNode* a, TreeNode* b) {
if (a->val != b->val) return a->val > b->val;
return a->height > b->height;
});
// 弹出末尾元素,为当前所选择的,用来构建新节点的两个节点
TreeNode* left = nodeList.back(); nodeList.pop_back();
TreeNode* right = nodeList.back(); nodeList.pop_back();
// 新节点的值为左右节点值的和
int val = left->val + right->val;
// 新节点的高度为左右节点的高度的较大值再+1
// 其中+1表示新节点增加的高度
int height = max(left->height, right->height) + 1;
// 构建新节点new_node
TreeNode* newNode = new TreeNode(val, left, right, height);
// 将新节点加入列表new_node中
nodeList.push_back(newNode);
}
}
// 中序遍历的函数
void inorder(vector<int>& ans, TreeNode* node) {
if (node == nullptr) return;
inorder(ans, node->left);
ans.push_back(node->val);
inorder(ans, node->right);
}
int main() {
int n;
cin >> n;
vector<int> lst(n);
for (int i = 0; i < n; ++i) {
cin >> lst[i];
}
// 初始化节点列表node_lst,包含为所有叶节点的列表
vector<TreeNode*> nodeList;
for (int val : lst) {
nodeList.push_back(new TreeNode(val, nullptr, nullptr, 0));
}
// 构建树,退出后node_lst的长度为1
buildTree(nodeList);
// 初始化答案列表
vector<int> ans;
// 中序遍历函数,传入根节点为node_lst中唯一的一个节点node_lst[0]
inorder(ans, nodeList[0]);
// 输出结果
for (int val : ans) {
cout << val << " ";
}
// 清理内存
for (TreeNode* node : nodeList) {
delete node;
}
return 0;
}时空复杂度
时间复杂度:O(N^2logN+M)。其中N为数组初始长度,M为最终树的节点数。
- 在构建树的函数中,每一次
while循环数组中的节点数减少1个,while循环所需时间复杂度为O(N),而循环中的单次排序时间复杂度为O(NlogN),故构建树的总时间复杂度为O(N^2logN)。 - 中序遍历树需要经过每一个节点,所需时间复杂度为
O(M)
空间复杂度:O(M)。
