2025A-流浪地球
题目描述与示例
题目描述
流浪地球计划在赤道上均匀部署了N个转向发动机,按位置顺序编号为0~N-1。
- 初始状态下所有的发动机都是未启动状态;
- 发动机启动的方式分为**“手动启动”和“关联启动”**两种方式;
- 如果在时刻
1一个发动机被启动,下一个时刻2与之相邻的两个发动机就会被“关联启动”; - 如果准备启动某个发动机时,它已经被启动了,则什么都不用做;
- 发动机
0与发动机N-1是相邻;
地球联合政府准备挑选某些发动机在某些时刻进行“手动启动”,当然最终所有的发动机都会被启动。
哪些发动机最晚被启动呢?
题目练习网址:https://www.algomooc.com/problem/P3709
输入描述
第一行两个数字N和E,中间有空格
N`代表部署发动机的总个数,`E`代表计划手动启动的发动机总个数`1<N<=1000`,`1<=E<=1000`,`E<=N接下来共E行,每行都是两个数字T和P,中间有空格
T`代表发动机的手动启动时刻,`P`代表此发动机的位置编号。`0<=T<=N`,`0<=P<=N输出描述
第一行一个数字N,以回车结束N代表最后被启动的发动机个数
第二行N个数字,中间有空格,以回车结束每个数字代表发动机的位置编号,从小到大排序
示例一
输入
8 2
0 2
0 6输出
2
0 4示例二
输入
8 2
0 1
1 7输出
2
4 5解题思路
示例解析及题目总分析
考虑示例二的过程
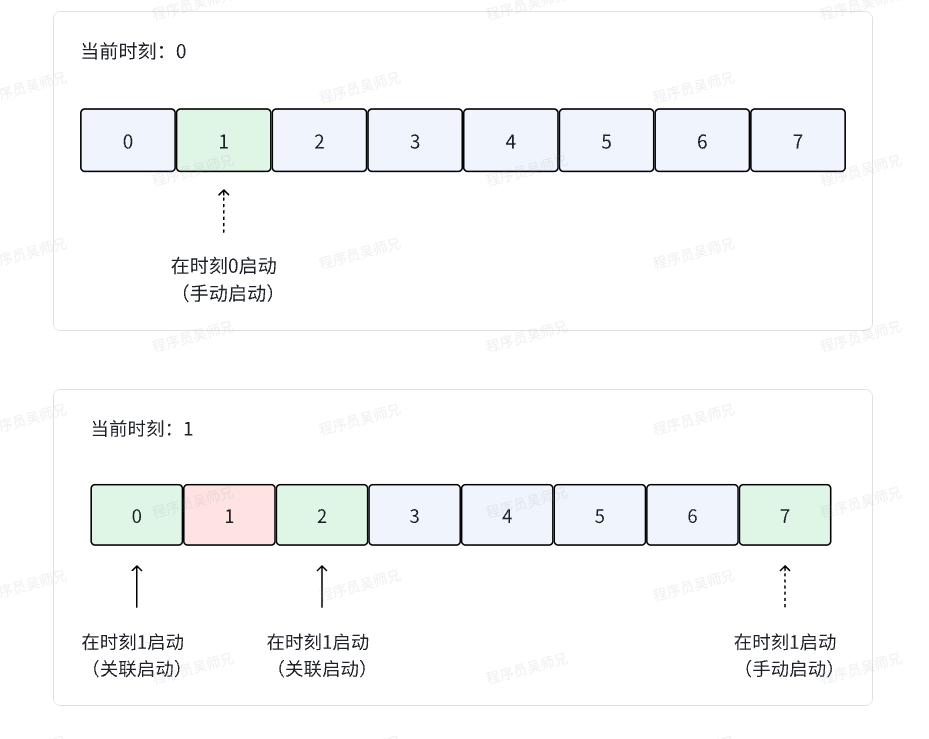
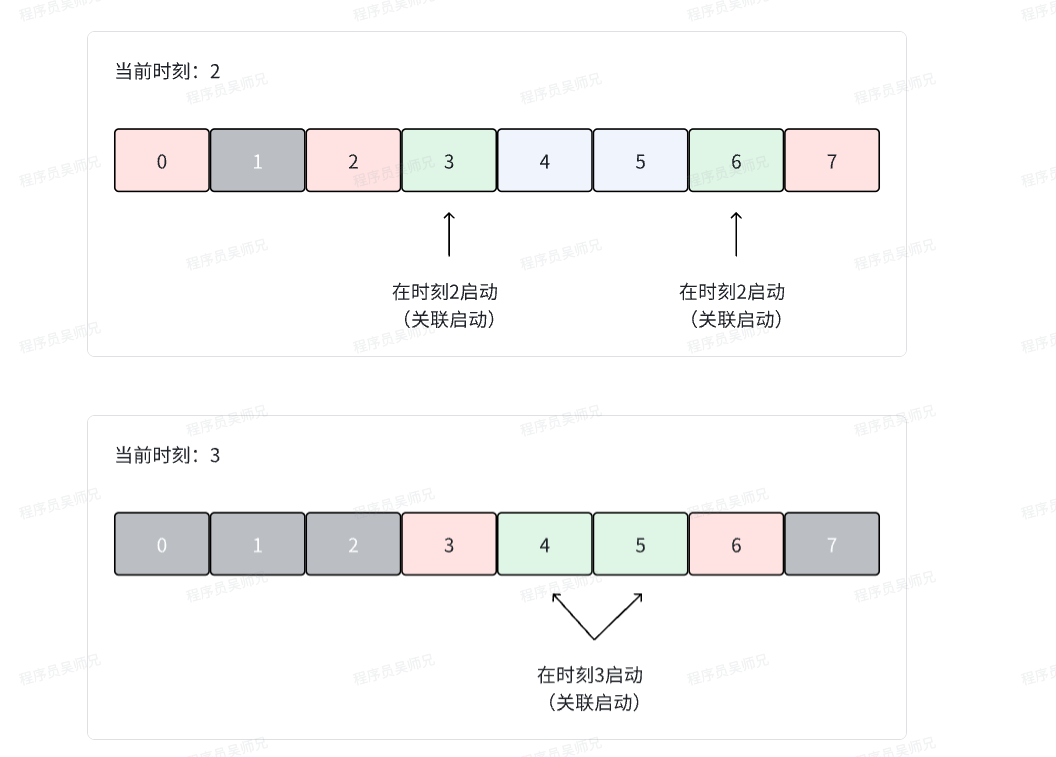
可以看到最后被启动的发动机是4和5。
首先我们可以比较快速地定位出这是一个BFS问题。
因为上一时刻启动的发动机,会使得其相邻的其他未启动发动机在下一个时刻启动。
这有点类似于病毒感染或者波纹传播等模型。
主要要解决两个问题:
- 这是一个1维环型数组,和我们经常遇到的二维网格模型有所不同
- 本题还存在时间先后的概念,某些发动机在中间的某些时刻会被手动启动(而不都是在最开始被启动)
把上述两个问题处理好,加以我们常用的BFS解题套路,本题其实不算难题。
处理一维环型数组
常规的二维网格DFS/BFS,在考虑近邻位置的时候,我们是取上下左右四个方向。
对于一维数组某一个元素的近邻位置,我们只需要考虑左右两个方向。
特别地,由于需要处理环型数组,我们在位置0和位置N-1需要进行额外判断。
可以构建函数get_neighbor()进行分类讨论,来获得元素x的两个近邻位置,即
def get_neighbor(x, N):
if x == 0:
return [N-1, 1]
elif x == N-1:
return [N-2, 0]
else:
return [x-1, x+1]或者使用取余的写法,即
def get_neighbor(x, N):
return [(x-1+N) % N, (x+1+N) % N]处理延时入队问题
另一个更加重要的问题是延时处理的问题。
由于同一个时刻启动的发动机可能不止一台,我们首先使用哈希表来储存所有手动启动的发动机的信息。
# 用哈希表储存E条手动启动信息,其中key为若干的启动时刻T
# value为在同一个T中启动的若干发动机P构成的列表
table = defaultdict(list)
# 遍历E条启动信息
for _ in range(E):
# 输入启动时刻T,发动机P
T, P = map(int, input().split())
# 将发动机编号P储存在启动时刻T对应的队列中
table[T].append(P)哈希表table中储存了所有手动启动的发动机信息。
其中key为若干的启动时刻T,value为在同一个T中启动的若干发动机P构成的列表。
譬如对于例子
8 4
0 1
1 7
1 5
3 0构建的哈希表为
table = {
0: [1],
1: [7, 5],
3: [0]
}我们知道,在BFS过程中的元素出队意味着我们要考虑其近邻元素的情况。
如果是不考虑延时入队的普通情况,我们会这样来完成BFS过程
total = 0
while total < N:
qSize = len(q)
total += qSize
if total == N:
ans = sorted(q)
break
for _ in range(qSize):
x = q.popleft()
for nx in get_neighbor(x, N):
if check_list[nx] == 0:
check_list[nx] = 1
q.append(nx)特别注意,total表示的是发动机的启动总数量。
在单层搜索下(同一个时刻的搜索),队列q中的所有元素都是在当前时刻要启动的发动机编号。
所以在当前时刻,total增加的量为qSize = len(q)。
为了找到最后一次启动的那些机器,我们可以多设置一个条件用来判断。
一旦发现total增加后数量为N,说明在这个时刻中队列q中的所有元素,就是最后启动的发动机编号,也就是答案。因此我们可以看到代码中存在
qSize = len(q)
total += qSize
if total == N:
ans = sorted(q)
break其中ans就是最终要输出的答案。
现在我们把延时入队的事情考虑进来。
在BFS过程中,我们可以设置一个变量cur_time,来表示当前进行到的时刻。
在进行到某一个时刻的时候,如果发现cur_time位于table中,意味着存在若干发动机是在这个时刻被手动启动的。这些发动机需要被加入到队列q中。即
if cur_time in table:
for x in table[cur_time]:
if check_list[x] == 0:
check_list[x] = 1
q.append(x)这部分代码必须加在更新total之前。
另外,每次while循环结束后,cur_time还需要递增1,表示整体的时刻增加。因此BFS过程的整体代码为
# 初始化发动机队列q为空队列
# 之所以没有和其他题一样进行队列初始化,是因为发动机的启动时刻是不确定的
# 第一个启动的发动机并不是一定从时刻0开始
q = deque()
# 构建check_list检查数组,长度为N,用于表示元素是否已经访问过
check_list = [0] * N
# 初始化发动机的启动个数total为cur_time个
total = 0
# 初始化当前时刻cur_time,取所有启动时刻中的最小值
# 这个地方初始化为0也没有错,只是后面的BFS过程会多进行几次循环
cur_time = min(list(table.keys()))
# 则如果还存在发动机尚未启动,应该继续进行BFS
# 由于循环中存在关于total == N的判断,这里写成while True也没错
while total < N:
# 如果在当前时刻cur_time,有若干发动机要【手动启动】,即cur_time位于哈希表table中
if cur_time in table:
# 考虑这些发动机编号x
for x in table[cur_time]:
# 如果x尚未检查过,说明还没有启动
if check_list[x] == 0:
# 那么将其在check_list设置为1,表示已检查过/已启动
check_list[x] = 1
# x加入队列,用来表示x在这个时刻启动
q.append(x)
# q中此时存在的元素,都是在当前时刻cur_time要启动的发动机编号
qSize = len(q)
# 当前时刻一共要启动qSize个发动机,total增加qSize
total += qSize
# 如果当前时刻启动完qSize个发动机之后,total到达N的数量
# 那么此时队列中的元素就是最后启动的那些发动机编号
# 取ans为q中元素排序后的结果所构成的列表
if total == N:
ans = sorted(q)
break
# 循环q中的qSize个发动机编号,考虑他们的近邻编号nx,近邻编号可能会被【关联启动】
for _ in range(qSize):
# 弹出队头中,在当前时刻启动的发动机编号x
x = q.popleft()
# 考虑x的近邻编号nx
for nx in get_neighbor(x, N):
# 如果nx尚未检查过,说明尚未启动
if check_list[nx] == 0:
# 那么将其在check_list设置为1,表示已检查过/已启动
check_list[nx] = 1
# nx入队,表示在下一个时刻中nx即将启动
q.append(nx)
# 单层BFS搜索完毕,当前时刻cur_time增加
# 此处cur_time也起到类似于搜索层数的意义
cur_time += 1代码
Python
# 欢迎来到「欧弟算法 - 华为OD全攻略」,收录华为OD题库、面试指南、八股文与学员案例!
# 地址:https://www.odalgo.com
# 华为OD机试刷题网站:https://www.algomooc.com
# 添加微信 278166530 获取华为 OD 笔试真题题库和视频
from collections import defaultdict, deque
# 在长度为N的环型数组中,对于编号x获得其两个近邻编号的函数
# 为了方便理解以下代码使用了三个if分支的写法
# 也可以使用取余函数,更加方便地写成一行即可
# return [(x-1+N) % N, (x+1+N) % N]
# 感兴趣的同学可以自行分析其逻辑
def get_neighbor(x, N):
if x == 0:
return [N-1, 1]
elif x == N-1:
return [N-2, 0]
else:
return [x-1, x+1]
# 输入数组长度N,启动信息条数E
N, E = map(int, input().split())
# 用哈希表储存E条储存信息,其中key为若干的启动时刻T
# value为在同一个T中启动的若干发动机P构成的列表
table = defaultdict(list)
# 遍历E条启动信息
for _ in range(E):
# 输入启动时刻T,发动机P
T, P = map(int, input().split())
# 将发动机编号P储存在启动时刻T对应的队列中
table[T].append(P)
# 初始化发动机队列q为空队列
# 之所以没有和其他题一样进行队列初始化,是因为发动机的启动时刻是不确定的
# 第一个启动的发动机并不是一定从时刻0开始
q = deque()
# 构建check_list检查数组,长度为N,用于表示元素是否已经访问过
check_list = [0] * N
# 初始化发动机的启动个数total为cur_time个
total = 0
# 初始化当前时刻cur_time,取所有启动时刻中的最小值
# 这个地方初始化为0也没有错,只是后面的BFS过程会多进行几次循环
cur_time = min(list(table.keys()))
# 则如果还存在发动机尚未启动,应该继续进行BFS
# 由于循环中存在关于total == N的判断,这里写成while True也没错
while total < N:
# 如果在当前时刻cur_time,有若干发动机要【手动启动】,即cur_time位于哈希表table中
if cur_time in table:
# 考虑这些发动机编号x
for x in table[cur_time]:
# 如果x尚未检查过,说明还没有启动
if check_list[x] == 0:
# 那么将其在check_list设置为1,表示已检查过/已启动
check_list[x] = 1
# x加入队列,用来表示x在这个时刻启动
q.append(x)
# q中此时存在的元素,都是在当前时刻cur_time要启动的发动机编号
qSize = len(q)
# 当前时刻一共要启动qSize个发动机,total增加qSize
total += qSize
# 如果当前时刻启动完qSize个发动机之后,total到达N的数量
# 那么此时队列中的元素就是最后启动的那些发动机编号
# 取ans为q中元素排序后的结果所构成的列表
if total == N:
ans = sorted(q)
break
# 循环q中的qSize个发动机编号,考虑他们的近邻编号nx,近邻编号可能会被【关联启动】
for _ in range(qSize):
# 弹出队头中,在当前时刻启动的发动机编号x
x = q.popleft()
# 考虑x的近邻编号nx
for nx in get_neighbor(x, N):
# 如果nx尚未检查过,说明尚未启动
if check_list[nx] == 0:
# 那么将其在check_list设置为1,表示已检查过/已启动
check_list[nx] = 1
# nx入队,表示在下一个时刻中nx即将启动
q.append(nx)
# 单层BFS搜索完毕,当前时刻cur_time增加
# 此处cur_time也起到类似于搜索层数的意义
cur_time += 1
# 退出BFS后,ans为最终的结果
print(len(ans))
print(*ans)Java
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 输入数组长度N和启动信息条数E
int N = scanner.nextInt();
int E = scanner.nextInt();
// 哈希表,用于存储启动信息,其中key为启动时刻T,value为启动的发动机列表
Map<Integer, List<Integer>> table = new HashMap<>();
// 遍历E条启动信息
for (int i = 0; i < E; i++) {
int T = scanner.nextInt();
int P = scanner.nextInt();
// 将发动机编号P添加到启动时刻T的列表中
table.computeIfAbsent(T, k -> new ArrayList<>()).add(P);
}
// 队列q,用于BFS
Deque<Integer> q = new ArrayDeque<>();
// 检查数组,用于标记发动机是否已经启动
boolean[] checkList = new boolean[N];
int total = 0; // 已启动发动机的总数
int curTime = Collections.min(table.keySet()); // 初始时刻
List<Integer> ans = new ArrayList<>();
// 进行BFS搜索,如果total小于N,则继续进行搜索
while (total < N) {
// 如果当前时刻有发动机要启动
if (table.containsKey(curTime)) {
// 考虑这些发动机编号
for (int x : table.get(curTime)) {
if (!checkList[x]) {
checkList[x] = true; // 标记为已启动
q.add(x); // 加入队列中
}
}
}
int qSize = q.size(); // 获取当前队列长度
total += qSize; // 更新已启动发动机的总数
// 如果启动的发动机数达到了总数量,说明所有发动机已启动
if (total == N) {
ans = new ArrayList<>(q); // 获取当前队列中的元素作为结果
Collections.sort(ans); // 对结果排序
break;
}
// 遍历当前时刻启动的所有发动机编号
for (int i = 0; i < qSize; i++) {
int x = q.poll(); // 弹出队列中的发动机编号
for (int nx : getNeighbors(x, N)) {
if (!checkList[nx]) {
checkList[nx] = true; // 标记为已启动
q.add(nx); // 加入队列中
}
}
}
curTime++; // 更新当前时刻
}
// 输出结果
System.out.println(ans.size());
for (int x : ans) {
System.out.print(x + " ");
}
}
// 获取环型数组中节点x的邻居节点
private static List<Integer> getNeighbors(int x, int N) {
List<Integer> neighbors = new ArrayList<>();
if (x == 0) {
neighbors.add(N - 1); // 左邻居
neighbors.add(1); // 右邻居
} else if (x == N - 1) {
neighbors.add(N - 2); // 左邻居
neighbors.add(0); // 右邻居
} else {
neighbors.add(x - 1); // 左邻居
neighbors.add(x + 1); // 右邻居
}
return neighbors;
}
}C++
#include <iostream>
#include <vector>
#include <unordered_map>
#include <deque>
#include <algorithm>
using namespace std;
// 获取环型数组中节点x的邻居节点
vector<int> getNeighbors(int x, int N) {
if (x == 0) return {N - 1, 1}; // 如果是第一个节点,则返回它的左右邻居
else if (x == N - 1) return {N - 2, 0}; // 如果是最后一个节点,则返回它的左右邻居
else return {x - 1, x + 1}; // 返回一般节点的左右邻居
}
int main() {
int N, E;
cin >> N >> E;
// 哈希表,用于存储每个启动时刻启动的发动机列表
unordered_map<int, vector<int>> table;
// 遍历每条启动信息
for (int i = 0; i < E; ++i) {
int T, P;
cin >> T >> P;
table[T].push_back(P); // 将发动机编号添加到相应的启动时刻中
}
deque<int> q; // 队列,用于BFS
vector<bool> checkList(N, false); // 用于标记发动机是否已经启动
int total = 0; // 已启动的发动机数量
int curTime = min_element(table.begin(), table.end(),
[](const auto& a, const auto& b) {
return a.first < b.first;
})->first; // 获取最早启动的时刻
vector<int> ans; // 存储结果的数组
// 进行BFS搜索,直到所有发动机都启动
while (total < N) {
if (table.find(curTime) != table.end()) {
// 如果当前时刻有发动机要启动
for (int x : table[curTime]) {
if (!checkList[x]) {
checkList[x] = true; // 标记为已启动
q.push_back(x); // 加入队列中
}
}
}
int qSize = q.size(); // 当前队列中的发动机数量
total += qSize; // 更新已启动的发动机数量
// 如果启动的发动机数达到了总数,则退出循环
if (total == N) {
ans.assign(q.begin(), q.end()); // 将队列中的元素赋值给结果数组
sort(ans.begin(), ans.end()); // 对结果进行排序
break;
}
// 遍历当前时刻启动的所有发动机编号
for (int i = 0; i < qSize; ++i) {
int x = q.front(); // 获取队列中的第一个发动机编号
q.pop_front(); // 从队列中删除该发动机编号
for (int nx : getNeighbors(x, N)) {
if (!checkList[nx]) {
checkList[nx] = true; // 标记为已启动
q.push_back(nx); // 加入队列中
}
}
}
curTime++; // 增加当前时刻
}
// 输出结果
cout << ans.size() << endl;
for (int x : ans) {
cout << x << " ";
}
return 0;
}C
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAXN 100000
// 用于存储启动时刻的发动机列表
typedef struct {
int *engines;
int count;
int capacity;
} EngineList;
// 获取邻居编号的函数
void get_neighbor(int x, int N, int neighbors[2]) {
if (x == 0) {
neighbors[0] = N - 1;
neighbors[1] = 1;
} else if (x == N - 1) {
neighbors[0] = N - 2;
neighbors[1] = 0;
} else {
neighbors[0] = x - 1;
neighbors[1] = x + 1;
}
}
// 动态添加到EngineList
void add_engine(EngineList *list, int engine) {
if (list->count == list->capacity) {
list->capacity *= 2;
list->engines = (int *) realloc(list->engines, list->capacity * sizeof(int));
}
list->engines[list->count++] = engine;
}
// 比较函数用于qsort
int compare(const void *a, const void *b) {
return *(int *)a - *(int *)b;
}
int main() {
int N, E;
scanf("%d %d", &N, &E);
// 初始化表格存储
EngineList table[1000]; // 假设启动时刻不超过1000
for (int i = 0; i < 1000; i++) {
table[i].engines = (int *) malloc(1 * sizeof(int));
table[i].count = 0;
table[i].capacity = 1;
}
// 读取启动信息
for (int i = 0; i < E; i++) {
int T, P;
scanf("%d %d", &T, &P);
add_engine(&table[T], P);
}
int check_list[MAXN] = {0}; // 记录是否已启动
int queue[MAXN], front = 0, back = 0; // 队列实现
int total = 0, cur_time = 0;
// 查找第一个启动时刻
while (table[cur_time].count == 0) {
cur_time++;
}
int *ans = NULL;
int ans_count = 0;
// BFS
while (total < N) {
// 如果在当前时刻cur_time,有发动机启动
for (int i = 0; i < table[cur_time].count; i++) {
int x = table[cur_time].engines[i];
if (!check_list[x]) {
check_list[x] = 1;
queue[back++] = x;
}
}
int qSize = back - front;
total += qSize;
if (total == N) {
ans = (int *) malloc(qSize * sizeof(int));
for (int i = 0; i < qSize; i++) {
ans[i] = queue[front + i];
}
ans_count = qSize;
qsort(ans, ans_count, sizeof(int), compare);
break;
}
for (int i = 0; i < qSize; i++) {
int x = queue[front++];
int neighbors[2];
get_neighbor(x, N, neighbors);
for (int j = 0; j < 2; j++) {
int nx = neighbors[j];
if (!check_list[nx]) {
check_list[nx] = 1;
queue[back++] = nx;
}
}
}
cur_time++;
}
// 输出结果
printf("%d\n", ans_count);
for (int i = 0; i < ans_count; i++) {
if (i > 0) printf(" ");
printf("%d", ans[i]);
}
printf("\n");
// 释放内存
for (int i = 0; i < 1000; i++) {
free(table[i].engines);
}
free(ans);
return 0;
}Node JavaScript
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
const input = [];
rl.on('line', (line) => {
input.push(line.trim());
});
rl.on('close', () => {
function getNeighbor(x, N) {
if (x === 0) {
return [N - 1, 1];
} else if (x === N - 1) {
return [N - 2, 0];
} else {
return [x - 1, x + 1];
}
}
const [N, E] = input[0].split(' ').map(Number);
// 用于存储启动时刻和发动机的关系
const table = new Map();
for (let i = 1; i <= E; i++) {
const [T, P] = input[i].split(' ').map(Number);
if (!table.has(T)) {
table.set(T, []);
}
table.get(T).push(P);
}
const checkList = new Array(N).fill(0); // 检查列表,0 表示未启动
const q = []; // 队列,用于存储当前启动的发动机编号
let total = 0; // 已启动的发动机总数
let curTime = Math.min(...table.keys()); // 初始化当前时刻为最早的启动时刻
let ans = [];
// BFS 主循环
while (total < N) {
// 手动启动的发动机
if (table.has(curTime)) {
for (const x of table.get(curTime)) {
if (checkList[x] === 0) {
checkList[x] = 1;
q.push(x);
}
}
}
const qSize = q.length;
total += qSize;
// 如果所有发动机都已启动
if (total === N) {
ans = q.slice().sort((a, b) => a - b);
break;
}
// 处理关联启动的近邻
for (let i = 0; i < qSize; i++) {
const x = q.shift();
for (const nx of getNeighbor(x, N)) {
if (checkList[nx] === 0) {
checkList[nx] = 1;
q.push(nx);
}
}
}
// 递增时间
curTime++;
}
console.log(ans.length);
console.log(ans.join(' '));
});Go
package main
import (
"bufio"
"fmt"
"os"
"sort"
"strconv"
"strings"
)
func getNeighbor(x, N int) []int {
if x == 0 {
return []int{N - 1, 1}
} else if x == N-1 {
return []int{N - 2, 0}
}
return []int{x - 1, x + 1}
}
func main() {
scanner := bufio.NewScanner(os.Stdin)
scanner.Scan()
firstLine := strings.Fields(scanner.Text())
N, _ := strconv.Atoi(firstLine[0])
E, _ := strconv.Atoi(firstLine[1])
// 使用 map 存储启动时刻和发动机编号
table := make(map[int][]int)
for i := 0; i < E; i++ {
scanner.Scan()
line := strings.Fields(scanner.Text())
T, _ := strconv.Atoi(line[0])
P, _ := strconv.Atoi(line[1])
table[T] = append(table[T], P)
}
checkList := make([]int, N) // 检查数组,0 表示未启动
q := []int{} // 队列,保存当前启动的发动机编号
total := 0 // 启动的发动机总数
curTime := int(1e9) // 当前时刻,初始化为一个大值
for t := range table {
if t < curTime {
curTime = t
}
}
var ans []int
// BFS 主循环
for total < N {
// 手动启动发动机
if starts, exists := table[curTime]; exists {
for _, x := range starts {
if checkList[x] == 0 {
checkList[x] = 1
q = append(q, x)
}
}
}
qSize := len(q)
total += qSize
// 如果所有发动机启动完毕
if total == N {
ans = make([]int, len(q))
copy(ans, q)
sort.Ints(ans)
break
}
// 处理关联启动的近邻
for i := 0; i < qSize; i++ {
x := q[0]
q = q[1:]
for _, nx := range getNeighbor(x, N) {
if checkList[nx] == 0 {
checkList[nx] = 1
q = append(q, nx)
}
}
}
// 递增时间
curTime++
}
fmt.Println(len(ans))
for i, v := range ans {
if i > 0 {
fmt.Print(" ")
}
fmt.Print(v)
}
fmt.Println()
}时空复杂度
时间复杂度:O(N+M)。N个元素都要出入队1次,while循环的M次,其中M为总搜索层数。
空间复杂度:O(N+T)。哈希表table和检查列表check所占空间。
