LeetCode 376、摆动序列

一、题目描述

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 **摆动序列 。**第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

• 例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
• 相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

提示：

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000

**进阶：**你能否用 O(n) 时间复杂度完成此题?

二、题目解析

具体操作如下：

1、每个元素都有三种状态，一开始都是 beginState。

2、如果当前元素的值大于它之前元素的值，那么说明当前元素处于上升阶段，状态设置为 upState。

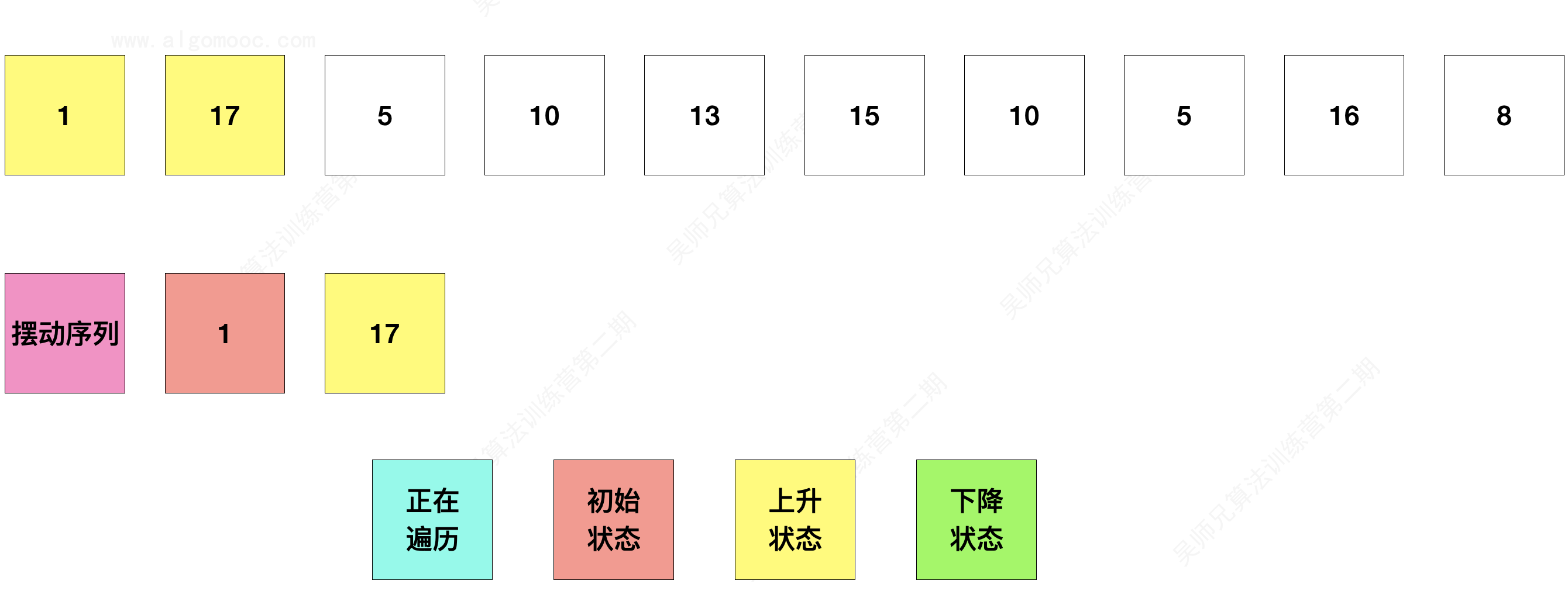
3、如果当前元素的值小于它之前元素的值，那么说明当前元素处于下降阶段，状态设置为 downState。

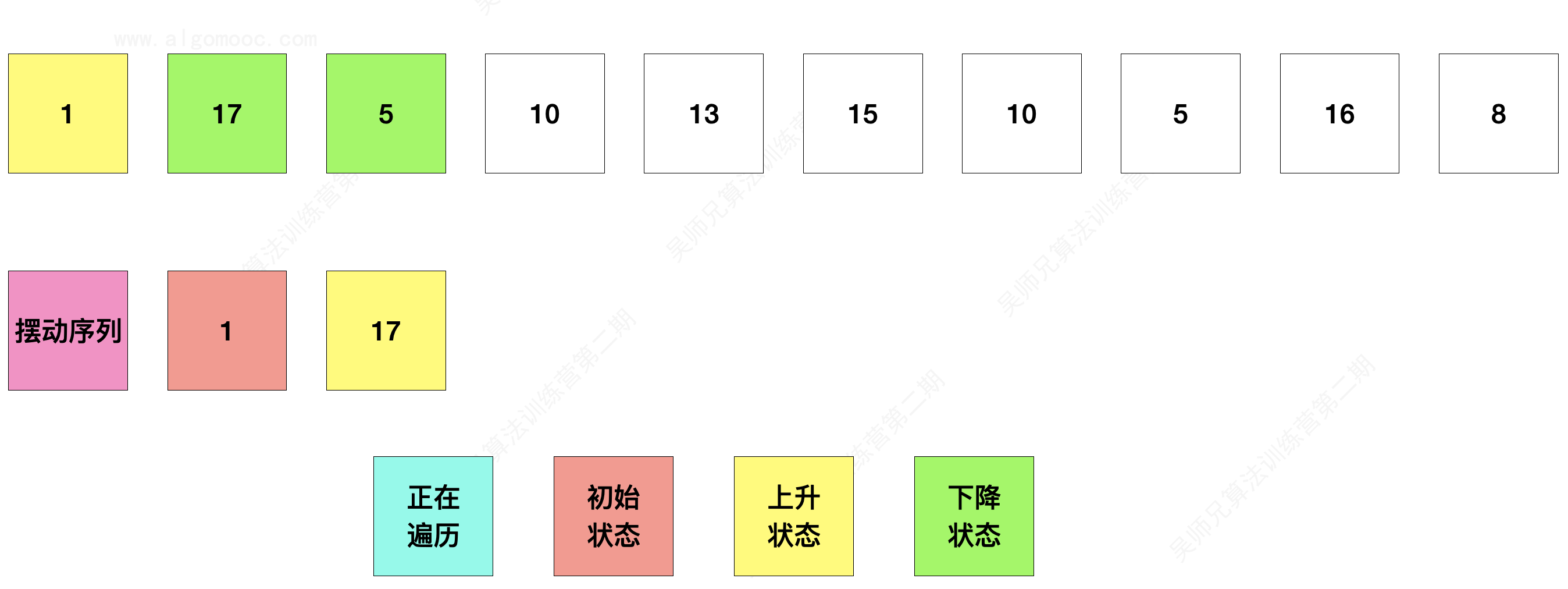
4、接下来，开始遍历 nums 中的所有元素，每个元素都有三种状态，在这三种状态下去判断这个元素应该怎么操作。

5、如果是在 begin 状态，那么比较 nums[i] 和 nums[i-1] 的大小。

• 1、如果 nums[i] > nums[i-1]，代表着现在处于上升过程，状态修改为 upState，摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1。

• 2、如果 nums[i] < nums[i-1]，代表着现在处于下降过程，状态修改为 downState，摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1。

6、如果是在 upState状态，说明 nums[i] 的前面两个元素 nums[i-2] < nums[i-1]，正在处于上升过程，只有此时 nums[i] < nums[i-1]，那么 nums[i-2]，nums[i-1]，nums[i] 这三者形成一个波峰才能摆动，并且状态修改为 downState。

7、如果是在 downState状态，说明 nums[i] 的前面两个元素 nums[i-2] > nums[i-1]，正在处于下降过程，只有此时 nums[i] > nums[i-1]，那么 nums[i-2]，nums[i-1]，nums[i] 这三者形成一个波谷才能摆动，并且状态修改为 upState。

三、参考代码

1、Java 代码

// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com
// 作者：程序员吴师兄
// 代码有看不懂的地方一定要私聊咨询吴师兄呀
// 摆动序列(376):https://leetcode-cn.com/problems/wiggle-subsequence/
class Solution {
    public int wiggleMaxLength(int[] nums) {
        
        // 每个元素都有三种状态

        // 1、每个元素的初始状态
        int beginState = 0;

        // 2、如果当前元素的值大于它之前元素的值
        // 比如 nums[i] > nums[i-1]
        // 那么说明当前元素处于上升阶段，状态设置为 up
        int upState = 1;


        // 3、如果当前元素的值小于它之前元素的值
        // 比如 nums[i] < nums[i-1]
        // 那么说明当前元素处于下降阶段，状态设置为 down
        int downState = 2;

        // 如果 nums 长度小于 2 
        if(nums.length < 2){
            // 由于仅有一个元素或者含两个不等元素的序列也视作摆动序列
            // 直接返回数组的长度
            return nums.length;
        }

        // 以第一个元素作为初始的摇摆序列，此时，长度为 1
        int length = 1;

        // 一开始，状态为 begin
        int state = beginState;

        // 接下来，开始遍历 nums 中的所有元素
        for( int i = 1 ; i < nums.length ; i++ ){
            // 每个元素都有三种状态，在这三种状态下去判断这个元素应该怎么操作

            // 1、如果是在 begin 状态
            if(state == beginState){
                // 那么比较 nums[i] 和  nums[i-1] 的大小

                // 此时的元素值为 nums[i]，它前面的元素值为 nums[i-1]
                // 如果 nums[i] > nums[i-1]，代表着现在处于上升过程
                if(nums[i] > nums[i-1]){
                    // 状态修改为 up
                    state = upState;
                    // 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length++;

                // 此时的元素值为 nums[i]，它前面的元素值为 nums[i-1]
                // 如果 nums[i] < nums[i-1]，代表着现在处于下降过程
                }else if(nums[i] < nums[i-1]){
                    // 状态修改为 down
                    state = downState;
                    // 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length++;
                }else{

                    // do nothing

                }

            // 2、如果是在 up 状态
            // 说明 nums[i] 的前面两个元素 nums[i-2] < nums[i-1]，正在处于上升过程
            }else if(state == upState){

                // 只有此时 nums[i] < nums[i-1]
                // 那么 nums[i-2]，nums[i-1]，nums[i] 这三者形成一个波峰  ^
                if(nums[i] < nums[i-1]){
                    
                    // 此时，由于 nums[i] < nums[i-1]，开始处于下降状态了
                    // 状态修改为 down
                    state = downState;
                    // 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length++;
                }else{
                     // do nothing
                }

            // 3、如果是在 down 状态
            // 说明 nums[i] 的前面两个元素 nums[i-2] > nums[i-1]，正在处于下降过程
            }else if(state == downState){

                // 只有此时 nums[i] > nums[i-1]
                // 那么 nums[i-2]，nums[i-1]，nums[i] 这三者形成一个波谷 V
                if(nums[i] > nums[i-1]){

                    // 此时，由于 nums[i] > nums[i-1]，开始处于上升状态了
                    // 状态修改为 up                    
                    state = upState;
                    // 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length++;
                }else{
                     // do nothing
                }
            }
        }

        // 返回结果 length
        // 不需要返回具体序列
        return length;

    }
}

2、C++ 代码

// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com
// 作者：程序员吴师兄
// 代码有看不懂的地方一定要私聊咨询吴师兄呀
// 摆动序列(376):https://leetcode-cn.com/problems/wiggle-subsequence/
class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        // 每个元素都有三种状态

        // 1、每个元素的初始状态
        int beginState = 0;

        // 2、如果当前元素的值大于它之前元素的值
        // 比如 nums[i] > nums[i-1]
        // 那么说明当前元素处于上升阶段，状态设置为 up
        int upState = 1;


        // 3、如果当前元素的值小于它之前元素的值
        // 比如 nums[i] < nums[i-1]
        // 那么说明当前元素处于下降阶段，状态设置为 down
        int downState = 2;

        // 如果 nums 长度小于 2 
        if(nums.size() < 2){
            // 由于仅有一个元素或者含两个不等元素的序列也视作摆动序列
            // 直接返回数组的长度
            return nums.size();
        }

        // 以第一个元素作为初始的摇摆序列，此时，长度为 1
        int length = 1;

        // 一开始，状态为 begin
        int state = beginState;

        // 接下来，开始遍历 nums 中的所有元素
        for( int i = 1 ; i < nums.size() ; i++ ){
            // 每个元素都有三种状态，在这三种状态下去判断这个元素应该怎么操作

            // 1、如果是在 begin 状态
            if(state == beginState){
                // 那么比较 nums[i] 和  nums[i-1] 的大小

                // 此时的元素值为 nums[i]，它前面的元素值为 nums[i-1]
                // 如果 nums[i] > nums[i-1]，代表着现在处于上升过程
                if(nums[i] > nums[i-1]){
                    // 状态修改为 up
                    state = upState;
                    // 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length++;

                // 此时的元素值为 nums[i]，它前面的元素值为 nums[i-1]
                // 如果 nums[i] < nums[i-1]，代表着现在处于下降过程
                }else if(nums[i] < nums[i-1]){
                    // 状态修改为 down
                    state = downState;
                    // 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length++;
                }else{

                    // do nothing

                }

            // 2、如果是在 up 状态
            // 说明 nums[i] 的前面两个元素 nums[i-2] < nums[i-1]，正在处于上升过程
            }else if(state == upState){

                // 只有此时 nums[i] < nums[i-1]
                // 那么 nums[i-2]，nums[i-1]，nums[i] 这三者形成一个波峰  ^
                if(nums[i] < nums[i-1]){
                    
                    // 此时，由于 nums[i] < nums[i-1]，开始处于下降状态了
                    // 状态修改为 down
                    state = downState;
                    // 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length++;
                }else{
                     // do nothing
                }

            // 3、如果是在 up 状态
            // 说明 nums[i] 的前面两个元素 nums[i-2] > nums[i-1]，正在处于下降过程
            }else if(state == downState){

                // 只有此时 nums[i] > nums[i-1]
                // 那么 nums[i-2]，nums[i-1]，nums[i] 这三者形成一个波谷 V
                if(nums[i] > nums[i-1]){

                    // 此时，由于 nums[i] > nums[i-1]，开始处于上升状态了
                    // 状态修改为 up                    
                    state = upState;
                    // 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length++;
                }else{
                     // do nothing
                }
            }
        }

        // 返回结果 length
        // 不需要返回具体序列
        return length;

    }
};

3、Python 代码

# 登录 AlgoMooc 官网获取更多算法图解
# https://www.algomooc.com
# 作者：程序员吴师兄
# 代码有看不懂的地方一定要私聊咨询吴师兄呀
# 摆动序列(376):https://leetcode-cn.com/problems/wiggle-subsequence/
class Solution:
    def wiggleMaxLength(self, nums: List[int]) -> int:
        # 每个元素都有三种状态

        # 1、每个元素的初始状态
        beginState = 0

        # 2、如果当前元素的值大于它之前元素的值
        # 比如 nums[i] > nums[i-1]
        # 那么说明当前元素处于上升阶段，状态设置为 up
        upState = 1


        # 3、如果当前元素的值小于它之前元素的值
        # 比如 nums[i] < nums[i-1]
        # 那么说明当前元素处于下降阶段，状态设置为 down
        downState = 2

        # 如果 nums 长度小于 2 
        if len(nums) < 2 :
            # 由于仅有一个元素或者含两个不等元素的序列也视作摆动序列
            # 直接返回数组的长度
            return len(nums)
        

        # 以第一个元素作为初始的摇摆序列，此时，长度为 1
        length = 1

        # 一开始，状态为 begin
        state = beginState

        # 接下来，开始遍历 nums 中的所有元素
        for i in range(1 ,len(nums)) :
            # 每个元素都有三种状态，在这三种状态下去判断这个元素应该怎么操作

            # 1、如果是在 begin 状态
            if state == beginState :
                # 那么比较 nums[i] 和  nums[i-1] 的大小

                # 此时的元素值为 nums[i]，它前面的元素值为 nums[i-1]
                # 如果 nums[i] > nums[i-1]，代表着现在处于上升过程
                if nums[i] > nums[i-1] :
                    # 状态修改为 up
                    state = upState
                    # 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length += 1

                # 此时的元素值为 nums[i]，它前面的元素值为 nums[i-1]
                # 如果 nums[i] < nums[i-1]，代表着现在处于下降过程
                elif nums[i] < nums[i-1] :
                    # 状态修改为 down
                    state = downState
                    # 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length += 1

            # 2、如果是在 up 状态
            # 说明 nums[i] 的前面两个元素 nums[i-2] < nums[i-1]，正在处于上升过程
            elif state == upState :

                # 只有此时 nums[i] < nums[i-1]
                # 那么 nums[i-2]，nums[i-1]，nums[i] 这三者形成一个波峰  ^
                if nums[i] < nums[i-1] :
                    
                    # 此时，由于 nums[i] < nums[i-1]，开始处于下降状态了
                    # 状态修改为 down
                    state = downState
                    # 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length += 1
            # 3、如果是在 up 状态
            # 说明 nums[i] 的前面两个元素 nums[i-2] > nums[i-1]，正在处于下降过程
            elif state == downState :

                # 只有此时 nums[i] > nums[i-1]
                # 那么 nums[i-2]，nums[i-1]，nums[i] 这三者形成一个波谷 V
                if nums[i] > nums[i-1] :

                    # 此时，由于 nums[i] > nums[i-1]，开始处于上升状态了
                    # 状态修改为 up                    
                    state = upState
                    # 摆动序列中增加了 nums[i] 这个元素，所以 length 需要加 1
                    length += 1

        # 返回结果 length
        # 不需要返回具体序列
        return length

四、复杂度分析

时间复杂度：O(n)，其中 n 是序列的长度。我们只需要遍历该序列一次。

空间复杂度：O(1)。我们只需要常数空间来存放若干变量。